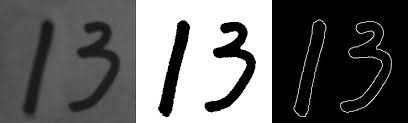Canny 算子是经典的边缘检测方法之一,目标不是“找所有灰度变化”,而是尽量找到定位准确、连续性好、噪声不敏感的真实边缘。它的核心思想可以概括为:先平滑抑噪,再计算梯度,随后只保留细而准的边,最后用双阈值把边连起来。
1)整体流程概览
Canny 边缘检测通常包括四步:
- 高斯滤波:抑制噪声
- 梯度计算:得到边缘强度与方向
- 非极大值抑制(NMS):把“粗边”细化为单像素
- 双阈值与滞后连接(Hysteresis):保留可靠边并连接断裂边
2)高斯滤波:为什么先模糊?
边缘检测本质依赖微分(梯度),而微分对噪声非常敏感:噪声会被放大成“伪边缘”。Canny 的第一步用高斯核 $G_\sigma$ 对图像 $I$ 做平滑:
$$I_s = G_\sigma * I$$
$\sigma$ 越大,平滑越强,噪声越少,但细小边缘也更容易被抹掉;$\sigma$ 越小,细节保留更好,但噪声更明显。
3)梯度计算:边缘强度与方向从哪来?
对平滑后的图像计算一阶导数(常用 Sobel 或高斯导数)得到 $x$、$y$ 方向梯度:
$$G_x=\frac{\partial I_s}{\partial x},\quad G_y=\frac{\partial I_s}{\partial y}$$
梯度幅值(边缘强度)与方向为:
$$M=\sqrt{G_x^2+G_y^2},\quad \theta=\arctan\left(\frac{G_y}{G_x}\right)$$
直观理解:
- $M$ 大说明灰度变化剧烈,可能是边;
- $\theta$ 表示边缘法向方向(梯度指向灰度上升最快方向)。
4)非极大值抑制:把“粗边”变成“细边”
仅靠梯度幅值,会得到一条“宽边”(边缘附近多个像素都有较大梯度)。Canny 希望边缘尽量细,所以做非极大值抑制(NMS):
- 对每个像素,沿梯度方向(即法向方向)比较两侧邻域的梯度幅值
- 如果当前像素不是局部最大值,就置为 0
常见实现会把方向 $\theta$ 量化到 $0^\circ$、$45^\circ$、$90^\circ$、$135^\circ$ 四类,方便取相邻像素比较。
结果:边缘从“带状”变成接近“单像素骨架”。
5)双阈值与滞后连接:既不漏边,也不多噪
NMS 后仍会有弱响应:有些是噪声,有些是真边缘在光照不均或反射变化下变弱的部分。Canny 用双阈值:
- $M \ge T_{high}$:强边缘(可靠)
- $T_{low} \le M < T_{high}$:弱边缘(不确定)
- $M < T_{low}$:抛弃
然后做滞后连接(Hysteresis):仅保留那些与强边缘连通的弱边缘(通常 8 邻域连通)。这样既能连接真实边缘中的断裂段(保连续),也能丢掉孤立弱响应(抑制噪声)。
6)参数怎么影响结果
- $\sigma$(高斯平滑强度):越大越抗噪,但细边更容易丢
- $T_{high}$:越高越“严格”,误检少但可能断边
- $T_{low}$:越低越容易连边,但太低会把噪声也接进来
经验上常见设置是 $T_{low}\approx(0.3\sim0.5)T_{high}$,但最佳值依赖图像对比度与噪声水平。