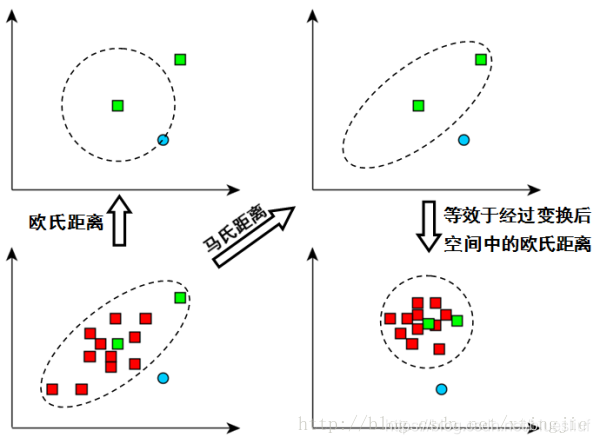
在做相似度、聚类或异常检测时,“距离”往往是最直接的度量方式。欧式距离最常见,但它在真实数据上容易产生偏差;马氏距离则是在考虑数据分布后更合理的一种替代。
1)欧式距离是什么
欧式距离衡量的是两点在特征空间中的直线距离:
$$ [ d(x,y)=\sqrt{\sum_{i=1}^{p}(x_i-y_i)^2} ] $$
它的优点是简单、直观、计算方便,适合特征尺度一致且相互独立的情况。
2)欧式距离的不足
(1)对尺度/量纲敏感
如果不同维度的数值范围差异很大(或方差差异明显),欧式距离会被“大尺度/大方差”的维度主导。此时你以为在比较“整体相似度”,实际可能只是某个维度在决定远近。
(2)忽略特征相关性
很多特征之间存在相关性(例如两个维度往往一起增大/减小)。欧式距离把它们当作独立维度处理,容易把“沿着常见相关方向的变化”也判得很远,从而高估差异或误判异常。
直观上:欧式距离的等距线是圆(高维是球),默认各方向同等重要、同等波动,但真实数据常呈“倾斜的椭圆云团”。
3)马氏距离是什么
马氏距离(Mahalanobis distance)衡量样本相对某个分布中心的“标准化偏离程度”:
$$ [ D_M(x)=\sqrt{(x-\mu)^T\Sigma^{-1}(x-\mu)} ] $$
- ($\mu$):数据均值(中心)
- ($\Sigma$):协方差矩阵(包含各维度方差与相关性)
- ($Sigma^{-1}$):用于“尺度校正 + 去相关”
它对应解决欧式距离的两大不足:
- 自动按方差缩放:波动大的方向,同样偏移不算太“远”;波动小的方向,小偏移也更“显著”。
- 自动考虑相关性:沿数据常见的相关方向变化距离更小,沿罕见方向变化距离更大。
几何上,马氏距离的等距线是与协方差一致的椭圆(高维是椭球),更贴合数据的真实分布形状。
4)总结
- 欧式距离:几何意义的直线距离,默认“同尺度、无相关”。
- 马氏距离:统计意义的距离,会根据方差与相关性调整,回答“在这类数据里偏离得有多不典型”。